[Kaggle] AIMO2 : Early Sharing Prize는 이미 나왔지만, (Qwen2.5, TIR, ToRA Paper 리뷰) [2]

목차

• Qwen2.5-Math-72B-Instruction
• ToRA의 TIR 
  • Imitation-Learning
  • Output Space Shaping
  • Result
  • Remaining Challenges
• 정리

Qwen2.5-Math-72B-Instruction

이번 대세는 Qwen의 Math 모델들이다. 아니 대세 정도가 아니고, 지배하고 있다.

가장 처음부터, ~10점 정도의 좋은 성적을 이끌어 나간건 바로 [Qwen2.5-Math-72B-Instruction] 모델을 활용한 방법론이었다. Qwen2.5-Math 모델들에 대한 자세한 내용은 [Qwen 블로그 글]을 확인하자.

블로그 글을 가볍게 정리하자면, 다음과 같다.

MATH Dataset Benchmark(Zero-shot@1 Acc)

위는 Open-Weight 모델들 중 MATH 데이터셋 벤치마크에 대한 성능이다. 이전에도 Qwen2-Math 모델들이 좋은 성능을 내고 있었지만, 한단계 더 개선되었다. 모델의 개선을 가져온 차이점은 무엇일까? 바로 TIR(Tool-Integrated Reasoning)방법을 적용했기때문이다.

ToRA의 TIR 

TIR은 문제를 해결하기 위해, 수식을 Python 코드(Python을 사용하지 않을 수 있지만, 대다수 모델과 데이터셋들이 Python코드로 되어있다.)로 구현하고, 그 코드를 실행하여 문제를 해결하도록 접근하는 방식이다.

가장 처음 제안된건 어딘지 모르겠지만, 처음 접한건 [ToRA:A Tool Integrated Reasoning Agent For Mathematical Problems Solving] 논문에서였다.

대회 시작에 접근법에 대해서 찾아보려고, AIMO - Prize1 우승 모델 HuggingFace의 Numina모델의 학습법에 대해서 공부하던 중에, MuMath-Code와 ToRA의 언급을 보고 논문을 접하게 되었다.

 

ToRA는 먼저 자연어를 이용한 추론을 진행하고, Tool 사용이 가능한 시점에 프로그램을 생성하여, 작업을 수행하고 그 결과물을 정답으로 사용하는 방식이다. 학습 단계는 먼저, LLM의 Tool-Integrated Reasoning(TIR)경로를 모방하도록 학습하는 Imitation-Learning과 위에서 학습한 모델을 이용해 TIR 경로를 더 규모가 큰 Teacher Model로 교정하고, 기존의 ToRA-Corpus와 합쳐서 표현력이 더 향상된 ToRA 모델을 학습하는 과정인 Output Space Shaping으로 진행된다.

 

Imitation-Learning

LLM을 활용한 ToRA-Corpus 생성

Imitation-Learning을 수행하기 위해, LLM을 활용해서 먼저 Corpus를 생성해야한다.

ToRA학습방법

LLM Inference TIR

 

SOTA LLM(GPT-4)을 활용하여, Tool-Integrated Reasoning 추론 결과물을 생성하는 과정을 위의 수식을 통해 보자.

1. LLM에 Prompt($p$), Problem($q$), 이전 Reasoning 경로($\tau_{i-1}$) 를 Concatenation을 입력으로, 답변을 생성한다. (처음 Reasoning 경로는 $\tau_0$으로, 빈칸이다.)
2. 만약, 생성 경로에 "\boxed{}"와 같은 Stop Criteria가 포함되어 있다면, 이전 Reasoning 경로($\tau_{i-1}$)과 이번 생성 답변($r_i$)를 Concat하여 반환한다. 아니라면, 이후 과정을 진행한다.
3. LLM을 활용하여, (1)번 과정에서 합친 전체 Prompt와 생성된 답변을 합쳐서, 문제 해결을 위한 Program을 생성한다.
4. 만약 "output`"과 같이 코드 실행을 위한 정지를 위한 Stop Criteria가 포함되었으면, 생성된 프로그램 코드를 외부 툴을 (Python Excution) 활용하여, 코드를 실행하여 나온 결과($o_i$)를 추가한다.
5. 이 과정을 최대 반복횟수($n$)만큼 반복하여, Reasoning 경로를 반환한다.

먼저 시중의 SOTA LLM(GPT-4)을 활용하여, 문제에 대한 정답을 생성하는 과정을 거친다. LLM에서 문제에 대한 답을 생성할 때 사용한 프롬프트는 다음과 같다.(사용한 프롬프트는 [microsoft/ToRA Repo]를 확인하면 된다.)

Integrate step-by-step reasoning and Python code to solve math problems
using the following guidelines:
- Analyze the question and write functions to solve the problem; the function should not take any arguments.
- Present the final result in LaTeX using a ‘\boxed{}‘ without any units.
- Utilize the ‘pi‘ symbol and ‘Rational‘‘ from Sympy for $\pi$ and fractions, and simplify all fractions and square roots without converting them to decimal values.

Here are some examples you may refer to:
---
Question: 
...

Solution:
[Solving Problem with CoT Generation example]

```python
[Problem Solving Code example]
```
```output
[Valid Python Code Result]
```

...
\boxed{}
---
Question:
...

 

프롬프트 전문을 보면, Few-Shot Examples 를 제공하여, 반환되는 답변의 형태를 추측할 수 있다. 순서대로, 'Instruction Prompt', 'Question', 'Solution', "'''python" (Solution 코드), "'''output"(코드의 실행결과), '\boxed{}'(최종 결과) 가 와야하는 것을 볼 수 있다.

 

Prompt 전문에 작성된 중요한 특징들을 보자

• 문제에 대한 자연어 분석이 포함되어 있다.
• 문제 풀이를 위한 Python 함수를 작성한다.
• Python 코드의 출력 결과물을 포함한다.(실행 오류나, 정답이 맞지 않는 코드를 검증한다.)
• LaTeX 문법을 사용하고, 최종 정답은 '\boxed{}'에 넣어서 표현한다.

생성 방식으로는 Greedy Decoding(Temperature: 0, N-Sampling: 1을 수행하고, 최대 반복수행 라운드($n$)는 3회로 제한했다. [ToRA LLM Inference API 코드]

코드의 오류가 있거나, 잘못된 정답을 생성한 것은 필터링하여, 총 16,000개의 ToRA-Corpus를 생성하고, 이 것을 이용해서 Imitation-Learning을 진행한다.

 

학습은 다음과 같이  진행된다.

Imitation Learning 학습 수식

Base Model $\mathcal{M}$를 이용해서 문제 $q$에 대해, 생성된 설명 $\tau_{i+1}a_{i+1}$에 대한 nll loss를 최소화하는 방향으로 학습을 진행한다. 

 

Output Space Shaping

ToRA-Corpus를 생성할 때, 문제 하나당 Tool을 사용한 정답을 한개만 갖고있기때문에, 모델의 "Output Space(출력 공간)"을 제한할 수 있기에, 유연성을 떨어트릴 수 있다. 따라서, 추론 단계를 다양화하고, 도구의 부적절한 사용을 줄이기 위해서, Output Space Shaping을 제안했다.

다양한 유효 경로를 찾기 위해서, 모방학습 모델 $\mathcal{M}을 이용해서, 각 문제 당 64개의 유효 경로를 샘플링했다. 또한 샘플이 중복되는 경우가 많았기에, 다양성을 더 높이고, 부적절한 행동들을 수정하기 위해 잘못된 경로도 활용하려고 했다.

 

잘못된 경로는 $\tilde{\tau}=l_1,...l_m$라인으로 이루어져있으며, $m$은 전체 라인의 수를 의미한다. 잘못된 경로의 선행 부분을 활용하여, 다시 규모가 더 큰 Teacher Model($\mathcal{M}\prime$)을 사용해서, Greedy Decoding으로 다시 경로를 생성한다.

$$\tau \leftarrow \mathbb{P}_{\mathcal{M}\prime}(\cdot|q \oplus \tilde{\tau}[:j])$$

이렇게 추가적으로 다시 생성한 경로 샘플들을 모델의 학습에 활용한다.

 

저자는 실험에서 Teacher Model로 항상 기존의 ToRA-Corpus로 훈련된 CodeLLaMA-34B를 활용했고, CodeLLaMA(7B~34B Imitation-Learning과 함께) 시리즈를 샘플링에 적용했다고 한다. 

 

Result

LLaMA-2, CodeLLaMA 시리즈를 ToRA-Corupus와 Output Space Shaping을 활용하여 학습했고, 각각의 결과물은 ToRA, ToRA-Code로 이름붙였다. 

Benchmark Results Table

Results on MATH subtopics

확실히 Code모델의 성능이 더 높게 나오는편이고, 저자는 아래와 같은 몇가지 결과들을 나열했다.

1. ToRA는 이전의 SOTA 모델을 넘어섰으며, 10개의 작업에서 13% ~ 19%의 절대적인 향상을 달성했다.
2. ToRA-70B는 ChatGPT(CoT, PAL 프롬프트)를 GSM8k(84.3% vs. 80.4%), MATH(49.7% vs. 38.7%)로 넘어섰고, ToRA-Code-34B는 GPT-4(with Code)의 MATH(50.7% vs. 51.8%)로 비교할 수 있는 수준이었다.
3. ToRA-Code는 동일한 사이즈의 ToRA보다 약 5% 높았다. 이를 통해 코드 데이터에 대해 학습된 것을 지속적으로 훈련하는게 Program Base로 문제를 해결하는데에는 더 도움이 된다.
4. WizardMath-70B를 보면, 이유 기반의 학습은 OOD 일반화에 오히려 독이 된다. -> LLaMA가 Base Model인데, 표 형식 추론과제(TabMWP)에서 57.5 vs. 49.8로 더 낮아짐. 근데 ToRA-70B는 이 TabMWP과제에서 74.0으로 효과적으로 일반화를 해냄.
5. ToRA는 Zero-shot 추론 속도도 빠르게 달성했으며, 문제 당 평균 1.02회의 Tool Interaction rounds를 기록하여 Tool 활용이 필요한 작업을 효과적으로 해결했다.

Each Formatting Results

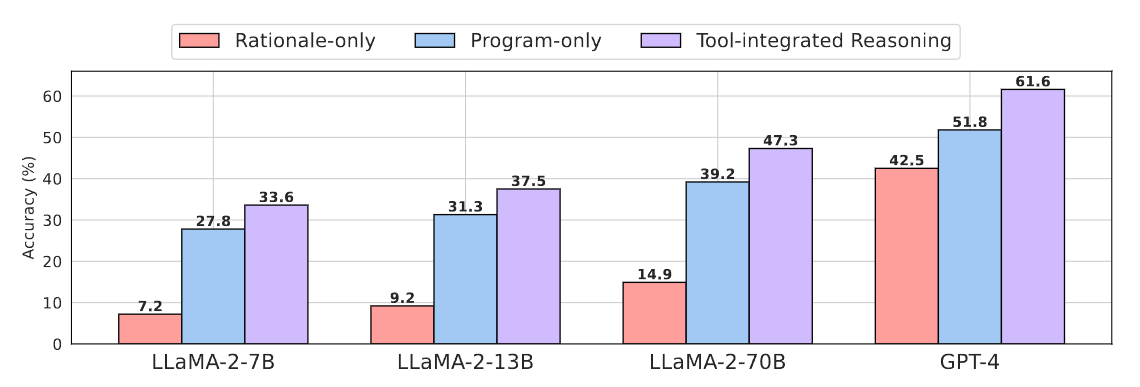
Formatting의 결과를 비교하기 위해서, (1)Rationale-only(e.g. CoT), (2)Program-only(e.g. PAL) (3)ToRA(TIR) 세가지 포맷팅 방식의 동일한 크기의 MATH 데이터셋으로 훈련된 GPT-4와 LLaMA-2의 정확도를 비교했다. 공정한 비교를 위해서, LLaMA-2모델은 output space shaping을 적용하지 않았다.

LLaMA-2모델은 ToRA방법은 Rationale-only, Program-only 방식에 비해 각각 29.0%, 6.7%의 개선이 있었다. 또한 GPT-4는 각각 19.1%, 9.8%의 개선이 있었다. 이를 통해 자연어를 통한 이유기반의 방식과 프로그램을 통합하는 효과가 있었다는 것을 보인다.

 

그럼 이제 Output Space Shaping방식은 어떤 효과를 보일까?

Output Space Shaping Results of CodeLLaMA

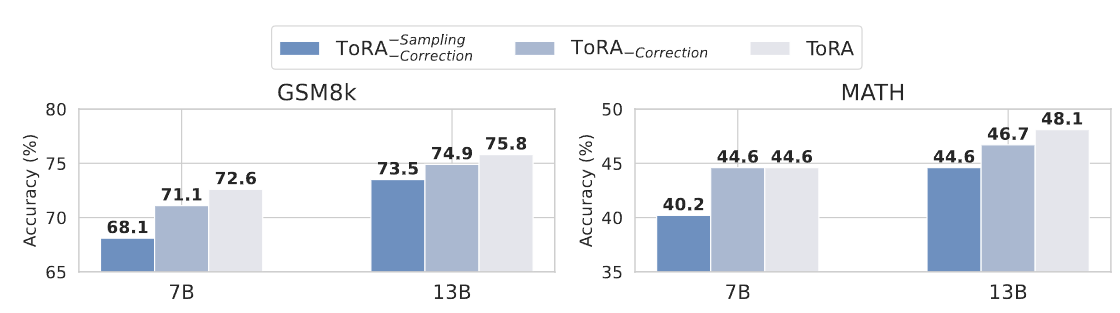
1. ToRA-Sampling, Correction : Shaping 없이 ToRA-Corpus로만 훈련
2. Tora-Correction : 문제당 최대 4개의 Valid Sampling 전략만 사용하여 훈련
3. ToRA :  문제당 최대 4개의 Valid Sampling 전략과 Correction을 모두 수행하여 훈련

로 변인을 조절해가며, 실험을 수행했다. 실험 결과는 다음과 같다.

• Output Space Shaping은 GSM8K, MATH에 대해서 각각 평균적으로 3.4%, 4.0%의 개선이 있었다. 또한 작은 모델에서 더 큰 이점이 있었다. -> GSM8K : 4.5%(7B) vs. 3.3%(13B), MATH : 4.4%(7B) vs. 3.5%(13B)
• Sampling 전략을 활용하면, 평균적으로 2.7%의 개선이 있었고, Correction을 포함하면 최대 4.5%의 개선 효과를 볼 수 있었다.
• Output Space Shaping은 가장 큰 모델인 70B에서도 효과가 있고, MATH에서 47.3%->49.7%로 눈에 띄는 개선이 있었다.

 

Remaining Challenges

그럼에도 ToRA에서 남아있는 도전 과제들이 있다. MATH Test Set에서 랜덤하게 100개에 대해 확인해봤다.

• Reasoing Error : 문제 해결 시에 잘못된 추론 단계나 조건을 놓치는 경우 - 38%
• Hallucination : 잘못된 숫자나 답을 생성하는 경우 - 5%
• Diagram Understanding : 입력된 도표를 잘못 해석하는 경우. 이건, 기하학, 미적분학, 중간 대수학에서 두드러지게 나타났는데, MATH 데이터셋에서 도형을 Asymptote 언어를 사용하여 텍스트로 설명하기에, 도형을 특수한 텍스트 설명만으로 이해하는데 어려움을 겪고 있는 것으로 파악된다. - 21%
• Inappropriate Tool Use : 도구를 올바르게 사용하지 못하는 경우 - 10%
• Syntax Error : 여러번 수정 시도에도, 지속적으로 발생하는 구문 오류 - 9%
• Runtime Error : 프로그램 실행 중 발생되는 오류로 재시도에도 해결되지 않음 - 9%
• Rationale-only Error : 근거가 올바르지 않고, 프로그램으로 형식화할 수 없음. - 3%
• False Negative : 맞는 정답인데, Ground Truth랑 완벽하게 일치하지 않는 경우 - 5%

성능을 크게 개선했지만, 아직 이러한 도전과제들이 남아있다.

각 문제점에 대해, 모든 예시 출력을 보여주기에는 공간이 너무 아까우니, 논문의 [F. Examples] 섹션에서 확인 가능하다.

 

Reasoning Error가 가장 일반적인 문제점이지만, Diagram Understanding은 모델의 학습으로 개선할 수 있지 않을까 하는 생각이 든다.

 

정리

뭐지.. Kaggle 해결과정 기록하다보니, Qwen2.5-Math 학습에 사용된, Tool-Integrated Reasoning(TIR)방법에 대한 논문 ToRA 논문 리뷰를 하게되었다. ToRA는 자연어와 프로그램을 통합하여, 모델이 수학문제를 해결할 때 성능을 효과적으로 개선했다.

 

다음엔, Early Sharing Prize를 획득한 Qwen/QwQ-32B-Preview 모델에 대해서 작성하게 되지 않을까싶다. 지금은 작성을 못한다. 학습한 방법이나, 어떤 레시피를 사용한지 알 수 있는게 거의 없다. 하지만, 요즘 오픈 소스 Reasoning 모델들의 추론 결과들을 보면, Self-Reflection, Self-Talking 과 같은 형태의 단어들이 많이 보인다. 또한 생성 토큰을 최대로 늘려, 자기 혼자 떠들어가며 문제를 해결해나가는 것을 볼 수 있다. 이건 따로 메모로 내가 파악한 인사이트를 기록해보려고 한다.

 

날이 갑자기 추워졌다. 눈은 저번에 아주 크게 오곤, 또 소식이 없지만 길가 물이 얼어서 위험할 수도 있으니, 갑자기 추워진 날에는 다들 조심하며 다니기를 바라겠씁니다. 감기도 조심하세요~ (감기 걸려서 조금 고생했습니다..)